Spatial data modeling
The problem almost inevitably encountered in spatio-temporal systems is uncertainty/imprecision. There are three basic approaches to spatial data uncertainty/imprecision modeling including exact models, probabilistic models, and fuzzy models.
However, current solutions do not offer a base for uncertain data representation relying upon a complete and consistent mathematical foundation and enabling sufficiently simple and effective models.
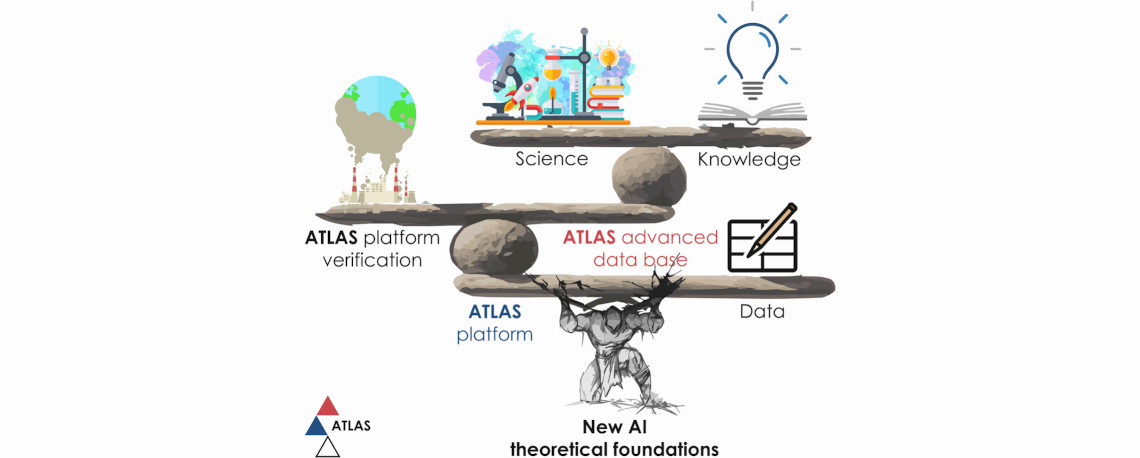
The ATLAS aspires to propose a theoretical base for simple, yet effective imprecise spatial data methods that satisfy the needs of diverse applications. The basis for spatial data modeling in this project is the linear fuzzy space theory that utilizes a fuzzy approach.
The theory provides the basis for simple yet effective uncertain/imprecise spatial data models exhibiting capacity for diverse applications. The proposed theoretical basis encompasses formal mathematical models of 2D fuzzy objects (point, line, segment, triangle, polygon, and circle), as well as corresponding fuzzy operations (intersection, union, translation, rotation, and fuzzy convex hull) and fuzzy relations (coincidence, containment, and orientation). The very same model applies to certain/precise data modeling as its special case.
Spatial processes modeling
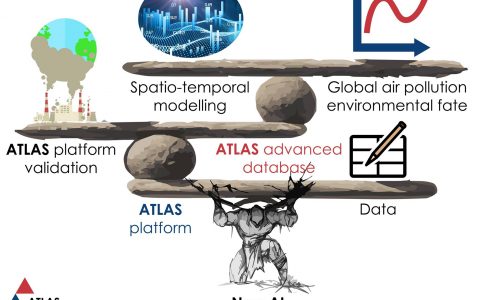
Spatio-temporal systems are mostly described by using various differential equations, but other modeling techniques are also involved, including time series, convolution, cellular automata, recently data-driven modeling, and even object-oriented modeling.
However, there is a lack of appropriate process models, especially when it comes to small-scale (regarding space) systems characterized by spatial and temporal uncertainty. Intending to address this issue, the ATLAS aspires to model a process as a set of interacting objects with behavior represented as a series of successive state transitions. In the case that some objects have spatial properties, the process is defined as a spatial process.
The fuzzy logic approach is utilized to capture uncertainty/imprecision in both spatial and temporal dimensions. Spatial processes are modeled using finite automaton, and procedural representation. A fuzzy object model of the process is proposed relying upon fuzzy finite automaton and fuzzy procedural representation. The proposed model integrates fuzzy finite automaton, fuzzy cellular automaton, and procedural way of representation.
For the purpose of the representation of the spatial process as a finite automaton, we define a fuzzy extension to common Finite Automaton (FA) and common Cellular Automaton (CA) definitions. The main feature of this representation is that a single object at the same time can be in more than one state with several membership degrees. In this case, a process is represented as a series of membership degrees. The system behavior can then be described by a declarative model, procedural model, or a combination of the two. For the purpose of transitions representation, the sets of fuzzy predicates are utilized for declarative representation, while for procedural representation transition function construction, are utilize fuzzy geometry transformations, such as translation, rotation, sharpening, blurring, etc.
Dynamical decision making under uncertainty
Many aggregation operators are used for modeling information fusion. It is very important to have a procedure for choosing the correct operator. Many important aggregation operators are constructed by integrals based on non-additive measures.
ATLAS aspires to model decisions under uncertainties where events or attributes are not independent (what is the usual requirement by probability modeling). Based on the conditional distributivity connection of a t-norm with respect to a t-conorm it was introduced in a hybrid probabilistic-possibilistic measure, which serves as a base for a maximal natural extension of von Neumann Morgenstern utility theory.
Distinct improvements in the current research approach
ATLAS will offer distinct improvements in the current research approach by the implementation of the extensive, publicly available, innovative research platform. The ATLAS platform is the first tangible outcome of such kind and a gateway to higher-level…
research analyses via centralized access to AI models, advanced data sharing, incorporated data processing tools and catalogs with descriptive metadata, and greater research interoperability and integration.
Ultimately, the ATLAS aspires to set up a framework that paves the way for further large flagship projects that will provide an effective response to current research challenges in different scientific fields, including, but not limited to: agriculture, energy, land development, tourism, climate change, health, and food protection, with environmental field and air pollution research being the first one.


 Overarching objectives
Overarching objectives